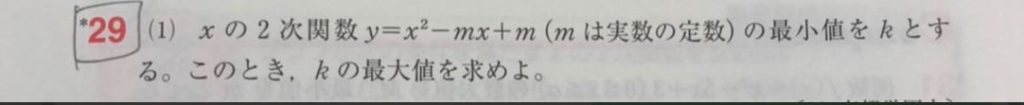
【質問】kはy座標のことなのになんで最大値があるんですか？

【回答】

2次関数　y = x^2 – mx + m (mは実数の定数）

x^2の係数は「1」（正の数）なのでグラフは下に凸の放物線になりますよね。
なのでこの関数の最小値「k」は、頂点のy座標になることが解ります。

あとは、定数「m」の値によって頂点の位置がずれるので、
その中でも最大値（グラフでいえば、一番上にいく）となる
場合を求める　ということになります。

m=1のときは、　y = x^2 – x + 1
m=2のときは、　y = x^2 – 2x + 2
m=-1のときは、 y = x^2 + x -1

と関数（グラフ）が変化しますよね。その中でも一番上にくる
場合を探っていきましょう。

---

問題文に惑わされた（kは最小値なのになぜ最大？？）ようだったので
問題の意味を整理するということで、ここまでを説明。

以降実際の解法は、自力でできたようです。

解法としては

・元の関数を平方完成させ頂点の座標を求めて解くか
・微分して「2x – m = 0」から解くか

のどちらかで解いてみましょう！